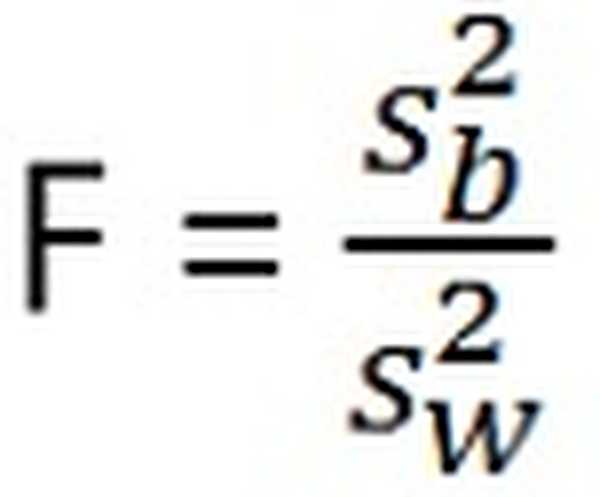Sự khác biệt giữa T-test và ANOVA
 Share
Share
 Có một ranh giới phân định mỏng giữa thử nghiệm t và ANOVA, tức là khi dân số chỉ có hai nhóm được so sánh, kiểm tra t được sử dụng, nhưng khi so sánh các phương tiện của hơn hai nhóm, ANOVA được ưa thích.
Có một ranh giới phân định mỏng giữa thử nghiệm t và ANOVA, tức là khi dân số chỉ có hai nhóm được so sánh, kiểm tra t được sử dụng, nhưng khi so sánh các phương tiện của hơn hai nhóm, ANOVA được ưa thích.
T-test và Phân tích phương sai được viết tắt là ANOVA, là hai kỹ thuật thống kê tham số được sử dụng để kiểm tra giả thuyết. Vì những điều này dựa trên giả định chung như dân số mà mẫu được rút ra nên được phân phối bình thường, tính đồng nhất của phương sai, lấy mẫu ngẫu nhiên của dữ liệu, tính độc lập của các quan sát, đo lường biến phụ thuộc theo tỷ lệ hoặc khoảng thời gian, mọi người thường hiểu sai hai.
Dưới đây, là một bài viết được trình bày để bạn hiểu sự khác biệt đáng kể giữa kiểm tra t và ANOVA, hãy xem.
Nội dung: T-test Vs ANOVA
- Biểu đồ so sánh
- Định nghĩa
- Sự khác biệt chính
- Phần kết luận
Biểu đồ so sánh
| Cơ sở để so sánh | Kiểm tra T | ANOVA |
|---|---|---|
| Ý nghĩa | Thử nghiệm T là một thử nghiệm giả thuyết được sử dụng để so sánh phương tiện của hai quần thể. | ANOVA là một kỹ thuật thống kê được sử dụng để so sánh các phương tiện của hơn hai quần thể. |
| Thử nghiệm thống kê | (x µ-Nhận) / (s / √n) | Giữa phương sai mẫu / Trong phương sai mẫu |
Định nghĩa kiểm tra T
Thử nghiệm t được mô tả là thử nghiệm thống kê kiểm tra xem liệu phương tiện dân số của hai mẫu có khác nhau nhiều hay không, sử dụng phân phối t được sử dụng khi độ lệch chuẩn không được biết và kích thước mẫu nhỏ. Nó là một công cụ để phân tích xem hai mẫu được rút ra từ cùng một quần thể.
Thử nghiệm dựa trên thống kê t, giả định rằng biến đó được phân phối bình thường (phân bố hình chuông đối xứng) và giá trị trung bình được biết và phương sai dân số được tính từ mẫu.
Trong giả thuyết t-test null có dạng H0: Ném (x) = Gian (y) chống lại giả thuyết thay thế H1: Tập (x) ≠ Tập (y), trong đó Tập (x) và Tập (y) đại diện cho phương tiện dân số. Mức độ tự do của kiểm tra t là n1 + n2 - 2
Định nghĩa của ANOVA
Phân tích phương sai (ANOVA) là một phương pháp thống kê, thường được sử dụng trong tất cả các tình huống trong đó so sánh được thực hiện giữa hơn hai quần thể có nghĩa là năng suất của cây trồng từ nhiều loại hạt giống. Nó là một công cụ phân tích quan trọng cho nhà nghiên cứu cho phép anh ta tiến hành kiểm tra đồng thời. Khi chúng tôi sử dụng ANOVA, giả định rằng mẫu được rút ra từ dân số phân phối bình thường và phương sai dân số là bằng nhau.
Trong ANOVA, tổng số lượng biến thể trong bộ dữ liệu được chia thành hai loại, tức là số tiền được phân bổ cho cơ hội và số tiền được gán cho các nguyên nhân cụ thể. Nguyên tắc cơ bản của nó là kiểm tra phương sai giữa các nhóm dân số bằng cách đánh giá mức độ biến đổi trong các mục của nhóm, tỷ lệ với lượng biến thể giữa các nhóm. Trong mẫu, phương sai là do sự xáo trộn ngẫu nhiên không giải thích được trong khi điều trị khác nhau có thể gây ra giữa phương sai mẫu.
Với việc sử dụng kỹ thuật này, chúng tôi kiểm tra, giả thuyết không (H0) trong đó tất cả các phương tiện dân số là như nhau, hoặc giả thuyết thay thế (H1) trong đó ít nhất một ý nghĩa dân số là khác nhau.
Sự khác biệt chính giữa thử nghiệm T và ANOVA
Sự khác biệt đáng kể giữa T-test và ANOVA được thảo luận chi tiết ở các điểm sau:
- Một thử nghiệm giả thuyết được sử dụng để so sánh phương tiện của hai quần thể được gọi là thử nghiệm t. Một kỹ thuật thống kê được sử dụng để so sánh các phương tiện của hơn hai quần thể được gọi là Phân tích phương sai hoặc ANOVA.
- Kiểm tra thống kê cho kiểm tra T là:
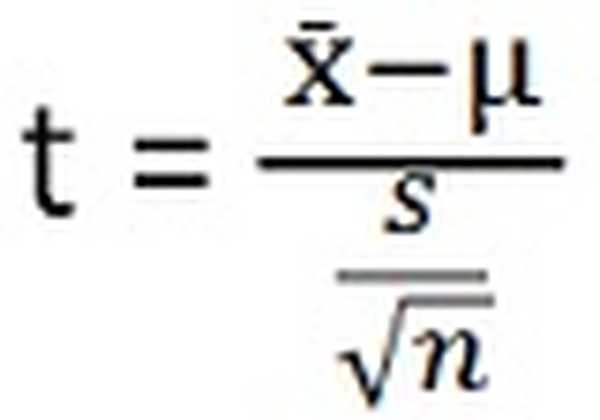 Thống kê kiểm tra cho ANOVA là:
Thống kê kiểm tra cho ANOVA là: 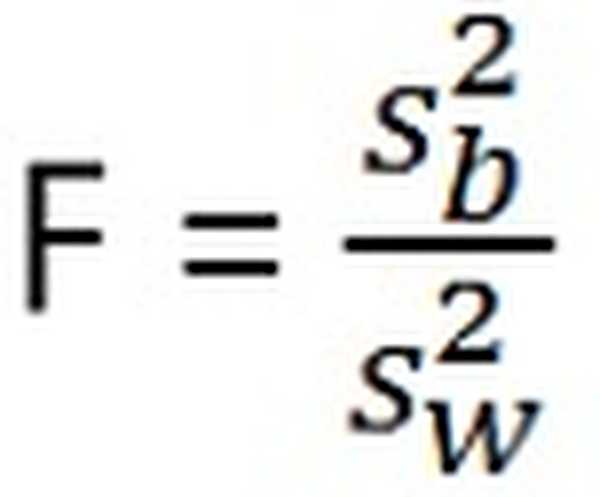
Phần kết luận
Sau khi xem xét các điểm trên, có thể nói rằng t-test là một loại ANOVA đặc biệt có thể được sử dụng khi chúng ta chỉ có hai quần thể để so sánh phương tiện của chúng. Mặc dù cơ hội lỗi có thể tăng nếu kiểm tra t được sử dụng khi chúng ta phải so sánh đồng thời hơn hai phương tiện của quần thể, đó là lý do tại sao ANOVA được sử dụng
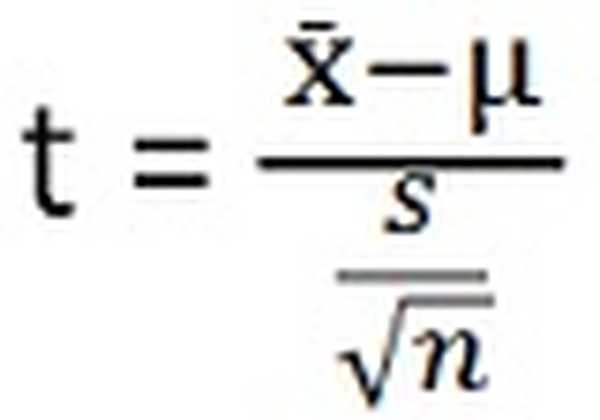 Thống kê kiểm tra cho ANOVA là:
Thống kê kiểm tra cho ANOVA là: